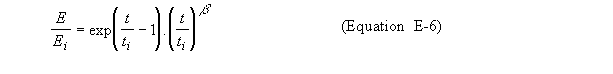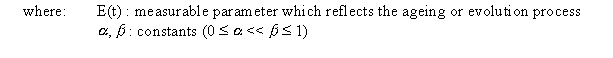System evolution kinetics

The following text is a renewed version of two published articles (Crevecoeur,1993,1994).

1. Concept of ageing or evolution kinetics

A system is defined as a group of many interlocking parts operating together with a common goal (after Forrester, 1968: "many" was added). This is a different definition than the usual, when people speak of systems of two components etc. Because of the many elements, some kind of "complexity" appears and one will rather call such systems "complex systems". A "macro-system" is defined by the huge difference of scale between the system and its unitary components: say factor one to 1 billion, or to 1 billion of billions or Avogrado's number. The unitary components may be assembled in subsystems. For instance, a piece of metal composed of atoms (assembled in grains), a cell composed of molecules (assembled in subunits of different functionalities), a body composed of cells (assembled in organs and subsystems) and an universe composed of stars (assembled in galaxies) are macro-systems. Here we will speak only of macro-systems and simply call them "systems". In order to be precise, we will define the class of systems we are studying as follows:

Definition of a system:A system is a collection of numerous interlocked subparts which is in a state of self-organized criticality such that it operates as a whole at an higher scale than that (those) of its subparts.

When subjected to operating conditions, the subparts and their interconnexions steadily reorganize in an adaptive process saving the integrity of the whole. The adequacy of the adaptive responses will depend on the system's internal organization and the material and energy available to carry out the solutions. The resulting ageing of the system can be modelized by the combination of many positive and negative first order feedback loops which occur in the subparts of the system when time elapses. Note that ageing is taken in the sense of an evolution or progress in time, without giving any qualitative value to these words: it is just the displacement of the system along the positive time axis in a quadri-dimensional space-time. The words ageing and evolution are thus considered to be synonyms in the present text. The feedback loops are the result of the step-by-step adaptation of the system to its operating conditions. The schematic view of a negative first order feedback loop is showed in Figure 1.

A very simple way to understand what happens is the following. The operating of the system results in internal challenges on the subparts which may jeopardize the system's integrity. The subparts have to adapt to the challenges in due time in order to allow further operation of the system as a whole. At each time, each subpart will modulate its available operating resources in a way to give the most appropriate response to the particular challenge it has to meet. The corresponding mathematical expression is given by Equation (1).

However, during operation, the challenges are not removed: they appear again and again, sometimes on a steady base sometimes not, with given kinetics depending on the operating constraints. It may happen that because of the kinetics or because of the kind of operation constraints, the adaptations in the subparts be sometimes non-standard even if satisfactory for the further operation of the system. The word "non-standard" means "different from what could be expected from the past behaviour". This may result in changes of information for neighbouring subparts about what their challenges are. Their responses could then also become non-standard. There will be a snowball effect: non-standard responses will induce differing assessments of the challenges which in turn will induce other non-standard responses. This corresponds to positive first order feedback loops as showed in Figure 2. The corresponding mathematical expression is an increasing exponential: see Equation (2). Indeed, supposing the increase in the number "z(t)" of non-standard responses at any time to be proportional to this number (i.e., existing non-standard responses are systematic sources of new non-standard response), one has : dz(t)/dt=a .z(t) - with : a = constant - which becomes Equation (2) after integration. Non-standard responses have no special value for the system. Sometimes, they will improve the system's organization, sometimes, they will hamper it locally.

The evolution of the system as a whole with time will be the resultant of multiple combinations of first order negative feedback loops (corresponding to local adaptive responses) and positive feedback loops (corresponding to local non-standard responses) on subparts.

Now, we have to take into account that the system is, by definition, in a state of self-organized criticality. Therefore, the intervals between adaptations will be statistically distributed according to a power law. This will be reflected by a decrease of parameter "b" in Equation (1) with an inverse power of time, the exponent being of the order of 1 to 2.

The combination of multiple negative and positive first order feedback loops taking account of self-organized criticality will lead to global evolution curves of the kind shown on Figure 3. This can be illustrated on a simple example. The resulting ageing kinetics of the system as a whole appears to follow three steps: (1) decrease - (2) near constancy - (3) increase of the ageing rate. The first step corresponds to what is usually observed as "learning". Many observations point to the fact that these three steps are always the same and in the same sequence.
It must be emphasized that the kind of curve given in Figure 3 is the envelope of the many internal processes which at each time increment combine negative and positive first order feedback loops on subparts.

An important consequence of the present approach is that the system ages even if all subparts remain operational. Indeed, ageing acts also on the interlinks (interconnexions) between subparts. These interlinks steadily reorganize in an adaptive way involved in saving the integrity of the whole. However small flaws can result from the process of steady reorganizations not only within the subparts but also for the interlinks themselves. These flaws will remain harmless as long as the integrity of the whole is saved. Though after a short or long time, the accumulation of many small flaws - distributed in an unpredictable way within the system - may result in global integrity loss leading to the collapse of the system. Therefore, proceeding to periodical maintenance actions (repair, replacement, ...) on the subparts in a Ť good-as-new ť approach - as is often performed for (electro-)mechanical devices and industrial plants - is not sufficient to avoid the ageing of the system.

Now, zooming onto small parts of the curve of Figure 3 will show irregular shapes as illustrated on Figure 3-1 for regions in the beginning and Figure 3-2 for regions at the end of the curve. The actual shape will depend on the particular set of combinations of negative and positive feedback loops for the system under consideration (see alternative values of parameters in the example).

2. Mathematical model to describe the evolution of systems

The typical 3-step curve of Figure 3 is well fitted by following equation:

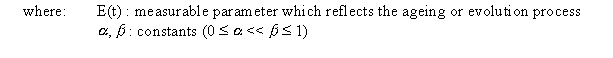
Indeed, the envelope curve of adaptation curves as given by Equation (1) taking account of self-organized criticality in time, will be a power law with an exponent less than unity.
When above equation is derived in function of time (expressed by a point "." above the parameter), one finds:

As will be illustrated in chapter 5, these two equations are basic to describe the ageing or evolution kinetics of systems. The reverse of parameter "a" gives the time scale of the ageing or evolution process. We will see that this time scale can be pretty different in function of the class of systems or particular evolution process considered. For one case we will have the whole ageing curve of Figure 3 in a few seconds, while for another case the process will last millions of years. Therefore, a period of observations too small compared to the time scale of the evolution process can occult part of the reality of the phenomenon. This must always be remembered. For instance, Figures 5, 6 and 7 show what Equation E-1 gives with identical values of the parameters but different time scales, that is, 1 000, 500 000 to 3 000 000 and 10 000 000 seconds, respectively. Only part of the learning stage is seen in Figure 5, while in Figure 6 we observe a quasi-linear behaviour typical for the second stage and Figure 7 shows the full curve.
Moreover, we see that systems following above equations will behave between two extremes:
(1) for a=0, E(t) reduces to the learning curve, i.e. it is purely polynomial: the subparts of the system adapt fully to their successive challenges ("they are not constrained towards non-standard responses") and there is no snowball effect
(2) for b=0, E(t) is purely exponential: non-standard responses accumulate exponentially (snowball effect) and there is no adaptation at all.
These two types of behaviour, polynomial and exponential, are encountered in several fields: reliability of systems, cosmology and biology.
Now let us further analyze the two equations of evolution. The three parameters a, b and K are constant as long as the physical constraints on the system remain constant. Let us explain this.
(1) The system has to operate under given conditions. In function of these conditions, the challenges on the subparts will vary of intensity. Severe operating conditions will induce challenges of higher intensity than mild operating conditions.
(2) Moreover, the intensity of the challenges on each subpart will also depend on the internal organization of the system. A better organization will allow better adaptations at each time increment and lower the risk that non-standard responses be given to the challenges.
(3) Finally, physics commands that ageing or evolution processes be temperature dependent (Arrhenius plots should be observed).
Let us call these three constraints: (1)the "stress S", (2) the "organization W" and (3) the "temperature T" respectively. We have thus three more equations:

The particular form of these equations must be determined for each class of systems, for instance experimentally by fixing two constraints and letting the third one vary. In some cases, this is already known thanks to extensive published test results (see, for instance, results of creep tests). Let us emphasize the meaning of the "stressS". In the present approach, the ageing or evolution kinetics of a system results from internal adaptations to operating conditions and possible environmental challenges which we called "constraints". What we usually observe is that these constraints induce stresses within the system, which we may describe as "distorsions threatening the internal organization of the system". The adaptations are related to the internal stresses rather than to the constraints directly. Identical constraints will induce different stresses, adaptations and ageing kinetics into systems of the same class but with different internal organization. The "stressS" quoted above is the resultant of all internal stresses at any time. It is therefore often difficult to quantify its level. It will sometimes be necessary to proceed by successive approximations based on experiments.

Now, as already mentioned, the reverse of parameter a gives the order of magnitude of the timescale for the ageing or evolution phenomenon. Let us analyze this more carefully. Physical processes that are described by growing exponentials are prone to become unstable when the exponent reaches the value of 1. Let us therefore define a "critical time t_i" such that t_i=1/a. The corresponding "critical ageing point", i.e., the point at which the ageing kinetics might become unstable, will be called "E_i".
Equation E-1 can then be re-written as Equation E-6. After t_i, the system will follow a path between sudden collapse and the continuation of the curve described by Equations E-1 or E-6. This zone has been shaded in, for instance, Figure 14. The actual collapse of an individual system will occur at a time "t_r" situated somewhere between the critical time "t_i" and the time "t_f " corresponding to the time necessary to reach the final evolution level if Equations E-1 and E-6 continued to be valid beyond t_i. The final evolution level corresponds to the exhaustion of the resources preventing any further evolution. After the critical time, the system usually no longer behaves as a cohesive whole adapting to its operation constraints but it continues to evolve. Along with the increase of number of non-standard responses there is an increase in incohesiveness: the system has lost its integrity. The non-standard responses occur more and more randomly and their distribution approaches a normal distribution.

3. Predictions using the model

Two kinds of predictions can be performed using the mathematical model of system evolution kinetics: (1) for a given system in operation ; (2) for a class of systems when the behaviour of several systems of the class is known. Of course, it is, at this stage, impossible to follow the particular responses of each subpart to its challenges when time proceeds. Therefore, it is not that kind of prediction which will be made that deduces the behaviour of the system from the knowledge of the behaviour of its subparts. It must be emphasized again that the equations used here reflect the global behaviour of the system no matter what happens precisely in the subparts: this global behaviour is the integration of all internal adaptations.

3.1 Predictions for a system

Equations E-1 & E-2 can be used.

The first thing to find out is which measurable parameter is the best one to reflect the global ageing or evolution of the system under scope. Often, several parameters are available. Experience teaches us which parameters can be used. Examples of such parameters are (see also the examples in Chapter 5): a cumulative number of failures, a growth parameter, any parameter known as reflecting variations in ageing level, like: resistance, force, strength, rapidity of reaction, deformation, etc. as they are defined in the different sciences. We will call this parameter the "evolution parameter" - E(t) in Equation E-1.

The second thing to check is whether the operational constraints "stress S", "organization W" and "temperature T" are - at least in average - constant.

The third thing to know is the order of magnitude of the timescale for the ageing or evolution process under scope.

When these three points are defined, the evolution parameter must be measured at successive time intervals significant with regard to the timescale (eg. tenths or hundredths of the timescale). The values of a, b and K are found by fitting the resulting curve with Equation E-1. The more experimental measurements are available, the better the fitting. Statistical means are used when there is some scattering. As soon as the value of a has stabilized, one can predict the critical time where the system's behaviour may become instable, i.e. the system may cease to operate as a whole. See several examples of fitting using Equation E-1.
As already seen, when critical points exist for systems, an alternative equation can be used to predict them. One just takes Equation E-1 rewritten in normalized form:

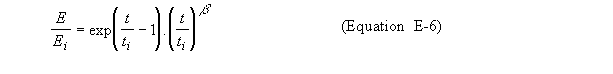
Again, it is sufficient to record the values of the evolution parameter at successive time intervals to find "E_i", "t_i" and "b". Several examples (see Figures 8, 9 and 10 ) show that the values of the predicted parameters "E_i" and "t_i" may stabilize sufficiently soon to allow useful predictions. The predicted times "t_i" are plotted against the successive times at which the predictions were made. A plateau is reached after a while. The value of "t_i" that is ultimately adopted is that of the intersection of the plateau with the straight line "t_i=t". This value can be approximated from the plateau value at about 80% to 90% of t_i in the examples shown. The approximation is the better the more time has elapsed.

It is noteworthy that parameters of Equations E-1 or E-6 are not defined from the beginning. They are fixed progressively with time as the adaptations proceed. No system will exactly behave as another one. There are small local differences in stress, temperature and organization and, even if they occur at levels several orders of magnitude below that of the system operating as a whole, due to the kinetics of the adjustments and the irreversibility of time, the differences will accumulate resulting in different evolution or ageing histories. However, after a time, the values of a and b will become fixed for a given system. It is easy to know when. Indeed, the curve corresponding to the derivative of Equation E-1 passes through a minimum at a time "t₂" given by Equation (4). a and b are then fixed and the critical time "t_i" can be deduced. It is interesting to notice that t₂/t_i only depends on b. Figure 12 shows the variation of 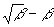with b. As b is usually comprised between 0.15 and 0.65 (Smith,1988, Crevecoeur,1992), the critical time t₂/t_i will lie between about 4 to 6.4 times t₂.

3.2 Predictions for a class of systems

In spite of different evolution stories, similar systems will statistically behave about the same way under the same constraints. We speak here of global behaviours resulting in similar evolution timescales. For instance, the creep of a steel at 1250°C (1523 K) will be of the order of a few seconds, while human life will be counted in decades. Therefore, when diagrams of the kind shown in Figure 13, giving for a class of systems the average value of the critical time in function of the stress and the temperature, are available, the critical time of a particular system pertaining to the class can be assessed from its operating constraints. Of course, in order to build diagrams of the kind of Figure 13, one must test several systems under rigourous operating conditions throughout their whole lifetime. For instance, to check the influence of temperature in a class of systems, one will first have to select several systems having the same organization "W". Then one has to submit these systems to exactly the same operational stress "S" maintained constant during their whole lifetime. Finally, this has to be done at a different temperature "T" for each system and again the temperature must be maintained constant during the whole lifetime of the system. This is not always possible: either because it is beyond our testing capabilities, or because there are too few systems, or for ethical reasons, etc. In addition, the sampling should be wide enough to allow validation through statistical analysis (average, standard deviation, etc.) And, last but not least, the stress resulting from operating is not always well defined or cannot exactly be reproduced for each equivalent system. Therefore, the availability of diagrams of the kind shown in Figure 13 is the exception. Anyway, in some cases, such diagrams exist and their number can only increase with the accumulation of experiments. One good example is the creep of metals because samples are abundant, the process of creep testing is well mastered and many tests have been performed for decades. But diagrams can also be obtained for other classes of systems when abundant series are available: devices manufactured in series(engines, etc.), populations of cells, bacteria, etc.

4. Other relationships derived from the model

Exponential and power (sometimes called "polynomial") laws are found in several fields, eg. reliability, creep, biology and cosmology. In mechanical system's reliability, an exponential law was proposed by Cox & Lewis (1966), while a power law was used to describe the learning curve (Duane,1964). In creep, one has, for instance, the power law given by Andrade(1910,1962) for the primary creep and the exponential law of Cottrell in the fifties. In addition, several well-known equations in creep (Norton, Monkman-Grant, Booker & al.) are found back using the theory. Also in biology, mortality rates are described either using an exponential law (Gompertz law,1825) or Weibull's equation (1951) for the failure rate, which, as already seen, is a power law. Finally, the two types of laws describing an evolution kinetics (exponential and polynomial) are also encountered in the time variation of the expansion parameter "R(t)" as deduced from several cosmological models: see the exponential models of Guth (1981), Albrecht & Steinhardt (1982) for an inflationary universe and several others (De Sitter, Dirac, Hoyle, Bondi etc.), while the classical model for the radiation-dominated era and the Einstein-De Sitter model give power laws. Equation E-1 can therefore be seen as conciliating both polynomial and exponential behaviours: power laws are found back when "a" is neglected, exponential laws when "b" is neglected.

5. Examples where the approach may be used

Let us see what observation teaches us. We have already seen that the system evolution kinetics approach could apply in several fields. They are recalled hereafter:

Mechanical systems reliability

Creep

Biology and Darwinian evolution

Cosmology

More fields of application might be found in the future. Let us anyway quote some connexions to theoretical concepts (self-organized criticality, Boltzmann's entropy, minimum entropy production theorem of Prigogine, etc.) in following item:

Statistical thermodynamics

Back to Home page